Introduction

Let's first illustrate how incremental computation looks like with an example similar to spreadsheet. First define a dependency graph like this:

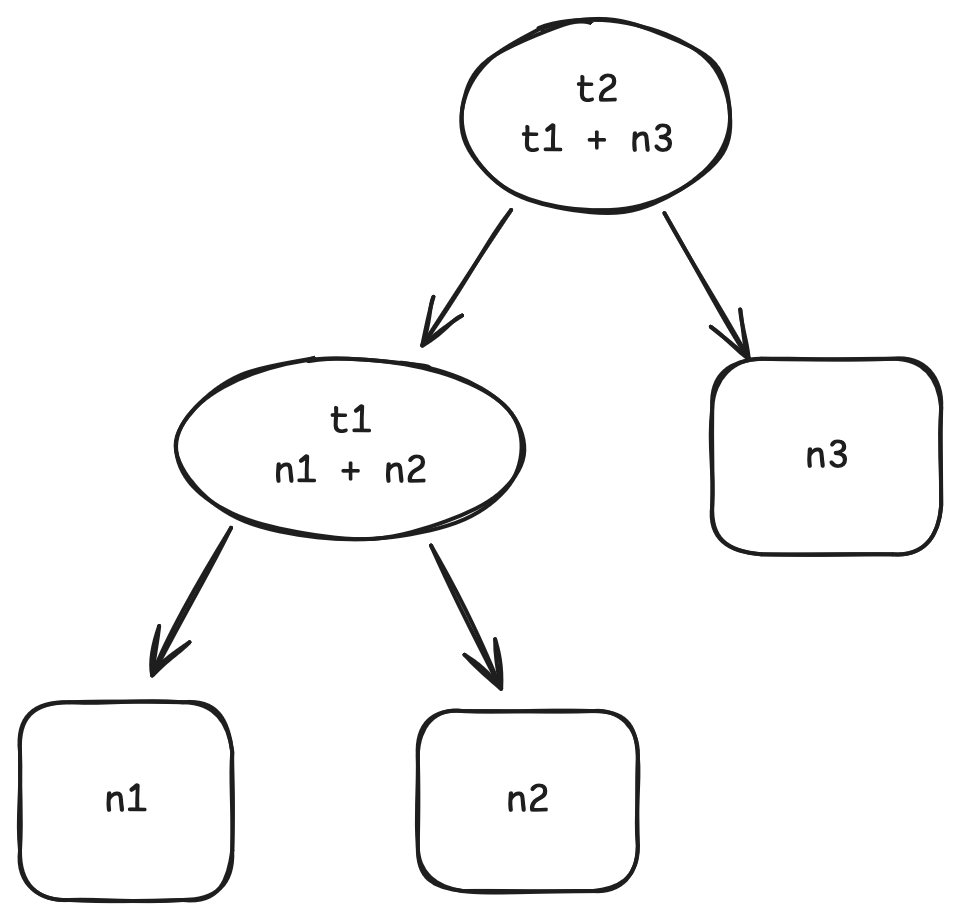
In this graph, t1's value is computed from n1 + n2 and t2's value is computed from t1 + n3.

When we want to get the value of t2, the computation defined in the graph will be done: first t1 is computed by n1 + n2, then t2 is computed by t1 + n3. This process is the same as non-incremental computation.

However, when we start to change values in n1, n2, or n3, things get different. Say we swap the value of n1 and n2, then get t2's value. In non-incremental computation, both t1 and t2 will be recomputed. But the computation of t2 is actually not needed, since all its dependency t1 and n3 are not changed (swap n1 and n2 wont change t1's value).

The following code example does exactly what we describe above. We use Cell::new to define n1, n2, and n3, which does not need computation. And Thunk::new to define t1 and t2 with computation.

test {
  // a counter to record the times of t2's computation
  let mut 
Int
cnt = 0
  // start define the graph
  let 
Cell[Int]
n1 = 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(value : Int) -> Cell[Int]
new(1)
  let 
Cell[Int]
n2 = 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(value : Int) -> Cell[Int]
new(2)
  let 
Cell[Int]
n3 = 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(value : Int) -> Cell[Int]
new(3)
  let 
Thunk[Int]
t1 = 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::
(thunk : () -> Int) -> Thunk[Int]
new(fn() {
    
Cell[Int]
n1.
(self : Cell[Int]) -> Int
get() 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 
Cell[Int]
n2.
(self : Cell[Int]) -> Int
get()
  })
  let 
Thunk[Int]
t2 = 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::
(thunk : () -> Int) -> Thunk[Int]
new(fn() {
    
Int
cnt 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= 1
    
Thunk[Int]
t1.
(self : Thunk[Int]) -> Int
get() 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 
Cell[Int]
n3.
(self : Cell[Int]) -> Int
get()
  })
  // get the value of t2
  
(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
  inspect(42, content="42")
  inspect("hello", content="hello")
  inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
Thunk[Int]
t2.
(self : Thunk[Int]) -> Int
get(), 
String
content="6")
  
(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
  inspect(42, content="42")
  inspect("hello", content="hello")
  inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
Int
cnt, 
String
content="1")
  // swap value of n1 and n2
  
Cell[Int]
n1.
(self : Cell[Int], new_value : Int) -> Unit
set(2)
  
Cell[Int]
n2.
(self : Cell[Int], new_value : Int) -> Unit
set(1)
  
(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
  inspect(42, content="42")
  inspect("hello", content="hello")
  inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
Thunk[Int]
t2.
(self : Thunk[Int]) -> Int
get(), 
String
content="6")
  // t2 does not recompute
  
(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
  inspect(42, content="42")
  inspect("hello", content="hello")
  inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
Int
cnt, 
String
content="1")
}

In this article, we will show how to implement an incremental computation library in MoonBit with the api used in the above example:

Cell::new
Cell::get
Cell::set
Thunk::new
Thunk::get

Problem Analysis and Solution

To implement the library, there are three main problems to solve:

Build up dependency graph on the fly

As a library in MoonBit, we don't have any easy ways to build up the dependency graph statically, since MoonBit does not have any meta programming mechanism currently. Therefore, we need to construct dependency graph on the fly. Since all we care about is what cells/thunks does a thunk depend on, a good option to build up dependency graph would be when user calls Thunk::get. Take the code above as an example:

let n1 = Cell::new(1)
let n2 = Cell::new(2)
let n3 = Cell::new(3)
let t1 = Thunk::new(fn() { n1.get() + n2.get() })
let t2 = Thunk::new(fn() { t1.get() + n3.get() })
t2.get()

When user calls t2.get(), we can know that at runtime t1.get() and n3.get() are called inside it. Therefore, t1 and n3 are dependencies of t2 and we can construct a subgraph:

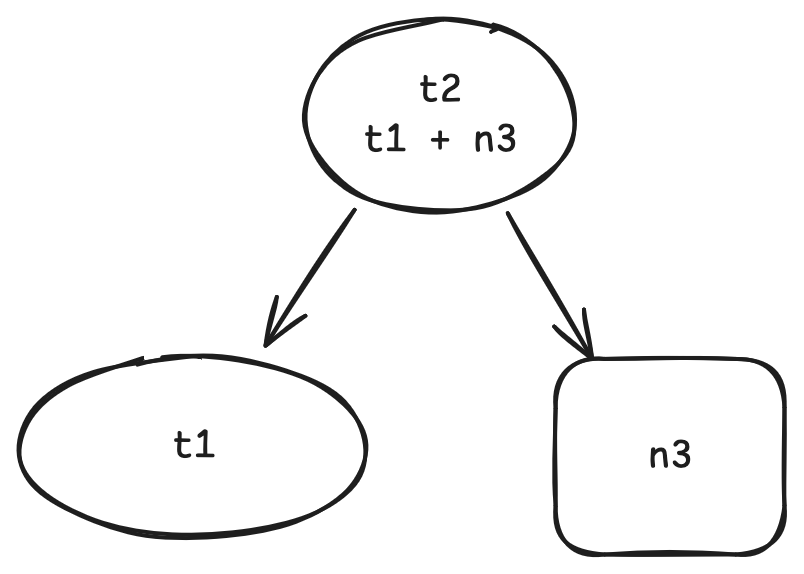
The same story will also happen when t1.get() is called inside t2.get().

So here is the plan:

1. we declare a stack to record which thunk are we currently getting. The reason we use stack here is that we are essentially record call stacks of every get.
2. whenever we call get, mark it as the dependency of stack top. If it's a thunk, push it onto stack.
3. whenever a thunk's get finished, pop it off the stack.

Let's see the full process of above example under this algorithm:

1. when we call t2.get, push t2 on the stack.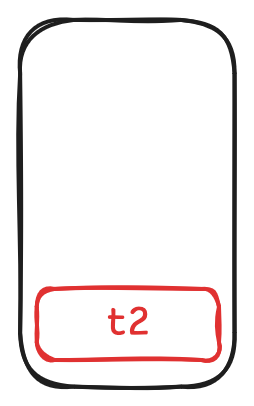

   

2. when we call t1.get inside t2.get, mark t1 as a dependency of t2 and push t1 onto the stack.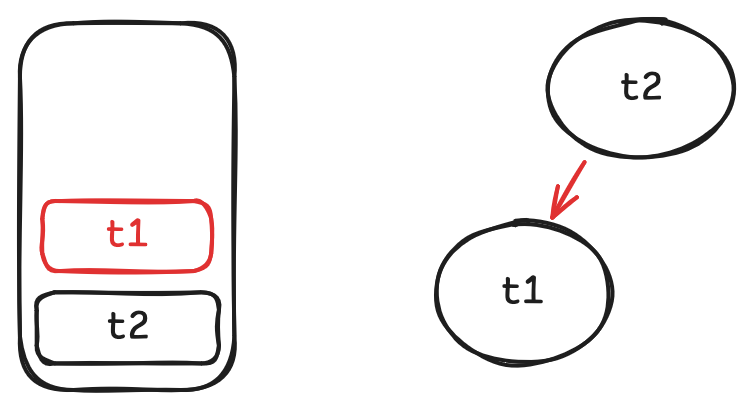

   

3. when we call n1.get inside t1.get, mark n1 as a dependency of t1.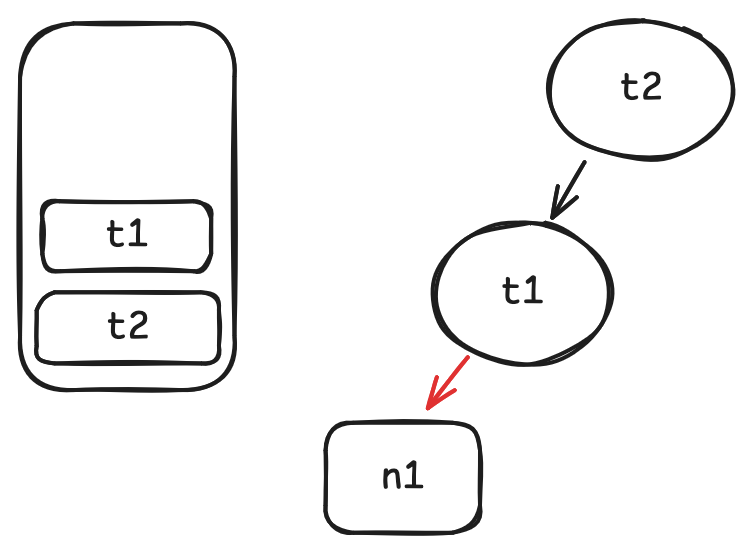

   

4. same story goes for n2.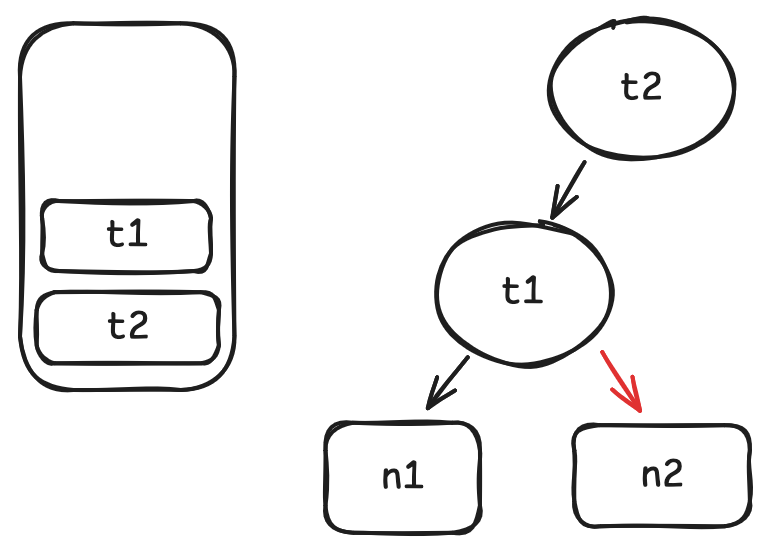

   

5. when t1.get finished, pop it from stack.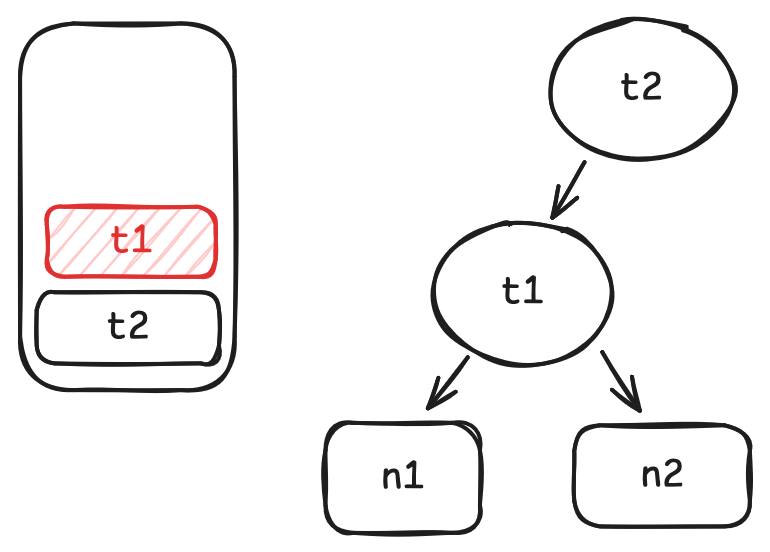

   

6. when we call n3.get, mark n3 as a dependency of t2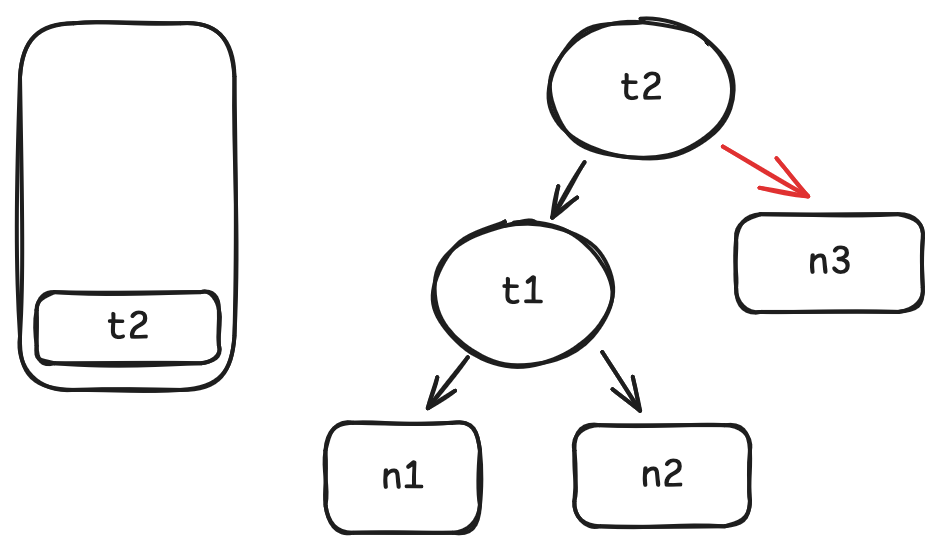

   

Besides the edge from dependent to dependency, we'd better also record an edge from dependency to dependent, so that we can easily traverse the graph backwards when we need.

In the code below, we'll use outgoing_edges to refer to edge from parent(dependent) to child (dependency) and incoming_edges to refer to the opposite.

A mechanism to mark outdated node

Whenever we call Cell::set, the node itself and all nodes depend on it should be marked as outdated. This will be one of the criteria to determine whether a thunk needs to be recomputed. This is generally a recursive backward traverse from a leaf of a graph. We can describe the process as pseudo MoonBit code:

fn dirty(node: Node) -> Unit {
  for n in node.incoming_edges {
    n.set_dirty(true)
    dirty(node)
  }
}

Determine whether a thunk needs to be recomputed

Whenever we call Thunk::get, we need to determine whether it really needs to be recomputed. But the dirty mechanism we describe in the last subsection is not enough. If we only use dirtiness to determine whether a thunk needs to be recomputed, there would be unneeded computation. Let's see it from the example we give at the beginning:

n1.set(2)
n2.set(1)
inspect(t2.get(), content="6")

After we swap the value of n1 and n2, n1, n2, t1, and t2 should all be marked as dirty, but when we call t2.get, there is no need to recompute t2, since the value of t1 does not change.

This reminds us that despite dirtiness, we need also to record whether a node's value differs from its last value. If a node is both dirty and one of its dependencies' value changed, it needs to be recomputed.

We can describe the algorithm as the pseudo MoonBit code below:

fn propagate(self: Node) -> Unit {
  // When a node is dirty, it might need to be recomputed
  if self.is_dirty() {
    // after recomputing, it's no longer dirty
    self.set_dirty(false)
    for dependency in self.outgoing_edges() {
      // recursively recompute every dependency
      dependency.propagate()
      // If a dependency's value changed, the node needs to be recomputed
      if dependency.is_changed() {
        // remove all outgoing_edges, since they will be reconstructed during evaluate
        self.outgoing_edges().clear()
        self.evaluate()
        return
      }
    }
  }
}

Implementation

Given the algorithms described in the last section, the implementation should be quite straightforward.

First, let's define Cell:

struct Cell[A] {
  mut 
Bool
is_dirty : 
Bool
Bool
  mut 
A
value : 
type parameter A
A
  mut 
Bool
is_changed : 
Bool
Bool
  
Array[&Node]
incoming_edges : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
}

Since Cell can only be leaf node in dependency graph, it does not have outgoing_edges. The trait Node here is used to abstract node in dependency graph.

Then, let's define Thunk:

struct Thunk[A] {
  mut 
Bool
is_dirty : 
Bool
Bool
  mut 
A?
value : 
type parameter A
A?
  mut 
Bool
is_changed : 
Bool
Bool
  
() -> A
thunk : () -> 
type parameter A
A
  
Array[&Node]
incoming_edges : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  
Array[&Node]
outgoing_edges : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
}

Thunk's value is optional, since it only exists after we first call Thunk::get.

We can easily add new for both types:

fn[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(value : A) -> Cell[A]
new(
A
value : 
type parameter A
A) -> 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] {
  
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::{
    
Bool
is_changed: false,
    
A
value,
    
Array[&Node]
incoming_edges: [],
    
Bool
is_dirty: false,
  }
}

fn[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::
(thunk : () -> A) -> Thunk[A]
new(
() -> A
thunk : () -> 
type parameter A
A) -> 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] {
  
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::{
    
A?
value: 
A?
None,
    
Bool
is_changed: false,
    
() -> A
thunk,
    
Array[&Node]
incoming_edges: [],
    
Array[&Node]
outgoing_edges: [],
    
Bool
is_dirty: false,
  }
}

Thunk and Cell are the two kinds of node in dependency graph, we can use the trait Node mentioned above to abstract them:

trait 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node {
  
(Self) -> Bool
is_dirty(
type parameter Self
Self) -> 
Bool
Bool
  
(Self, Bool) -> Unit
set_dirty(
type parameter Self
Self, 
Bool
Bool) -> 
Unit
Unit
  
(Self) -> Array[&Node]
incoming_edges(
type parameter Self
Self) -> 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  
(Self) -> Array[&Node]
outgoing_edges(
type parameter Self
Self) -> 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  
(Self) -> Bool
is_changed(
type parameter Self
Self) -> 
Bool
Bool
  
(Self) -> Unit
evaluate(
type parameter Self
Self) -> 
Unit
Unit
}

And implement the trait for both types:

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(self : Cell[A]) -> Array[&Node]
incoming_edges(
Cell[A]
self) {
  
Cell[A]
self.
Array[&Node]
incoming_edges
}

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(_self : Cell[A]) -> Array[&Node]
outgoing_edges(
Cell[A]
_self) {
  []
}

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(self : Cell[A]) -> Bool
is_dirty(
Cell[A]
self) {
  
Cell[A]
self.
Bool
is_dirty
}

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(self : Cell[A], new_dirty : Bool) -> Unit
set_dirty(
Cell[A]
self, 
Bool
new_dirty) {
  
Cell[A]
self.
Bool
is_dirty = 
Bool
new_dirty
}

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(self : Cell[A]) -> Bool
is_changed(
Cell[A]
self) {
  
Cell[A]
self.
Bool
is_changed
}

impl[A] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A] with 
(_self : Cell[A]) -> Unit
evaluate(
Cell[A]
_self) {
  ()
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A]) -> Bool
is_changed(
Thunk[A]
self) {
  
Thunk[A]
self.
Bool
is_changed
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A]) -> Array[&Node]
outgoing_edges(
Thunk[A]
self) {
  
Thunk[A]
self.
Array[&Node]
outgoing_edges
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A]) -> Array[&Node]
incoming_edges(
Thunk[A]
self) {
  
Thunk[A]
self.
Array[&Node]
incoming_edges
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A]) -> Bool
is_dirty(
Thunk[A]
self) {
  
Thunk[A]
self.
Bool
is_dirty
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A], new_dirty : Bool) -> Unit
set_dirty(
Thunk[A]
self, 
Bool
new_dirty) {
  
Thunk[A]
self.
Bool
is_dirty = 
Bool
new_dirty
}

impl[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A] with 
(self : Thunk[A]) -> Unit
evaluate(
Thunk[A]
self) {
  
Array[&Node]
node_stack.
(self : Array[&Node], value : &Node) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
Thunk[A]
self)
  let 
A
value = (
Thunk[A]
self.
() -> A
thunk)()
  
Thunk[A]
self.
Bool
is_changed = match 
Thunk[A]
self.
A?
value {
    
A?
None => true
    
(A) -> A?
Some(
A
v) => 
A
v 
(x : A, y : A) -> Bool
!= 
A
value
  }
  
Thunk[A]
self.
A?
value = 
(A) -> A?
Some(
A
value)
  
Array[&Node]
node_stack.
(self : Array[&Node]) -> &Node
Removes and returns the last element from the array.
Parameters:

array : The array from which to remove and return the last element.
Returns the last element of the array before removal.
Example:
  let arr = [1, 2, 3]
  inspect(arr.unsafe_pop(), content="3")
  inspect(arr, content="[1, 2]")
unsafe_pop() |> 
(t : &Node) -> Unit
Evaluates an expression and discards its result. This is useful when you want
to execute an expression for its side effects but don't care about its return
value, or when you want to explicitly indicate that a value is intentionally
unused.
Parameters:

value : The value to be ignored. Can be of any type.
Example:
  let x = 42
  ignore(x) // Explicitly ignore the value
  let mut sum = 0
  ignore([1, 2, 3].iter().each((x) => { sum = sum + x })) // Ignore the Unit return value of each()
ignore
}

The only complicated implementation is Thunk's evaluate. Here we need first to push the thunk on stack for dependency recording. node_stack is defined as below:

let 
Array[&Node]
node_stack : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node] = []

Then do the real computation and compare it with the last value to update self.is_changed. is_changed is used later to determine whether we need to recompute a thunk.

dirty and propagate are almost the same as the pseudo code described above:

fn 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::
(self : &Node) -> Unit
dirty(
&Node
self : &
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node) -> 
Unit
Unit {
  for 
&Node
dependent in 
&Node
self.
(&Node) -> Array[&Node]
incoming_edges() {
    if 
(x : Bool) -> Bool
Performs logical negation on a boolean value.
Parameters:

value : The boolean value to negate.
Returns the logical NOT of the input value: true if the input is false,
and false if the input is true.
Example:
  inspect(not(true), content="false")
  inspect(not(false), content="true")
not(
&Node
dependent.
(&Node) -> Bool
is_dirty()) {
      
&Node
dependent.
(&Node, Bool) -> Unit
set_dirty(true)
      
&Node
dependent.
(self : &Node) -> Unit
dirty()
    }
  }
}

fn 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::
(self : &Node) -> Unit
propagate(
&Node
self : &
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node) -> 
Unit
Unit {
  if 
&Node
self.
(&Node) -> Bool
is_dirty() {
    
&Node
self.
(&Node, Bool) -> Unit
set_dirty(false)
    for 
&Node
dependency in 
&Node
self.
(&Node) -> Array[&Node]
outgoing_edges() {
      
&Node
dependency.
(self : &Node) -> Unit
propagate()
      if 
&Node
dependency.
(&Node) -> Bool
is_changed() {
        
&Node
self.
(&Node) -> Array[&Node]
outgoing_edges().
(self : Array[&Node]) -> Unit
Clears the array, removing all values.
This method has no effect on the allocated capacity of the array, only setting the length to 0.
Example
  let v = [3, 4, 5]
  v.clear()
  assert_eq(v.length(), 0)
clear()
        
&Node
self.
(&Node) -> Unit
evaluate()
        return
      }
    }
  }
}

With all the foundation we build, the three main api: Cell::get, Cell:set, and Thunk::get are easy to implement.

To get value from a cell, it's simply just return the value filed in struct. But before that, we need first record it as a dependency if it's called inside Thunk::get.

fn[A] 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(self : Cell[A]) -> A
get(
Cell[A]
self : 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A]) -> 
type parameter A
A {
  if 
Array[&Node]
node_stack.
(self : Array[&Node]) -> &Node?
Returns the last element of the array, or None if the array is empty.
Parameters:

array : The array to get the last element from.
Returns an optional value containing the last element of the array. The
result is None if the array is empty, or Some(x) where x is the last
element of the array.
Example:
  let arr = [1, 2, 3]
  inspect(arr.last(), content="Some(3)")
  let empty : Array[Int] = []
  inspect(empty.last(), content="None")
last() is 
(&Node) -> &Node?
Some(
&Node
target) {
    
&Node
target.
(&Node) -> Array[&Node]
outgoing_edges().
(self : Array[&Node], value : &Node) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
Cell[A]
self)
    
Cell[A]
self.
Array[&Node]
incoming_edges.
(self : Array[&Node], value : &Node) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
&Node
target)
  }
  
Cell[A]
self.
A
value
}

Whenever we set a cell, we need to first make sure that the two states is_changed and dirty are updated correctly. Then mark every dependent as dirty.

fn[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::
(self : Cell[A], new_value : A) -> Unit
set(
Cell[A]
self : 
struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[
type parameter A
A], 
A
new_value : 
type parameter A
A) -> 
Unit
Unit {
  if 
Cell[A]
self.
A
value 
(x : A, y : A) -> Bool
!= 
A
new_value {
    
Cell[A]
self.
Bool
is_changed = true
    
Cell[A]
self.
A
value = 
A
new_value
    
Cell[A]
self.
(self : Cell[A], new_dirty : Bool) -> Unit
set_dirty(true)
    
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::
(&Node) -> Unit
dirty(
Cell[A]
self)
  }
}

In Thunk::get, similar to Cell::get, we first need to record self as a dependency. After that we pattern match on self.value. If it's None, it means that this is the first time user tries to get the thunk's value, so we can safely just evaluate it. If it's Some, we use propagate to make sure that we only recompute thunks that's really needed.

fn[A : 
trait Eq {
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::
(self : Thunk[A]) -> A
get(
Thunk[A]
self : 
struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[
type parameter A
A]) -> 
type parameter A
A {
  if 
Array[&Node]
node_stack.
(self : Array[&Node]) -> &Node?
Returns the last element of the array, or None if the array is empty.
Parameters:

array : The array to get the last element from.
Returns an optional value containing the last element of the array. The
result is None if the array is empty, or Some(x) where x is the last
element of the array.
Example:
  let arr = [1, 2, 3]
  inspect(arr.last(), content="Some(3)")
  let empty : Array[Int] = []
  inspect(empty.last(), content="None")
last() is 
(&Node) -> &Node?
Some(
&Node
target) {
    
&Node
target.
(&Node) -> Array[&Node]
outgoing_edges().
(self : Array[&Node], value : &Node) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
Thunk[A]
self)
    
Thunk[A]
self.
Array[&Node]
incoming_edges.
(self : Array[&Node], value : &Node) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
&Node
target)
  }
  match 
Thunk[A]
self.
A?
value {
    
A?
None => 
Thunk[A]
self.
(self : Thunk[A]) -> Unit
evaluate()
    
(A) -> A?
Some(_) => 
trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::
(&Node) -> Unit
propagate(
Thunk[A]
self)
  }
  
Thunk[A]
self.
A?
value.
(self : A?) -> A
Extract the value in Some.
If the value is None, it throws a panic.
unwrap()
}

Reference

• Adapton: Composable, demand-driven incremental computation, PLDI 2014 original paper of adapton
• illusory0x0/adapton.mbt adapton library in MoonBit